Likt's Blog

天空一直都在，是云来了又去。

0%

实现图的深度优先和广度优先遍历

发表于 更新于 分类于 ， 阅读次数： Valine：
本文字数： 9.8k 阅读时长 ≈ 18 分钟
在邻接表/邻接矩阵表示法的基础上实现图的深度优先和广度优先遍历，实现图的最小生成树算法。

实验六 图及其应用

一、实验目的

1) 加深对图这一数据结构的理解，学习利用图来表示和解决实际问题。
2) 在掌握邻接表/邻接矩阵表示法的基础上实现图的深度优先和广度优先遍历。
3) 掌握图的最小生成树算法。

二、实验内容

1) 在邻接表/邻接矩阵的基础上实现图的深度优先遍历和广度优先遍历操作，并输出遍历结果。
2) 某公司拟建一个局域网，需要连接6栋楼（0，1，2，3，4，5），其地理分布如下图1所示，各边上的权值代表楼宇间距离。
设计要求：根据下图中的楼宇分布，设计出布线造价最小的局域网络图，要求连接所有的顶点，并且总的布线费用最低。
实验提示：要想布线造价最小，可将图中各顶点间的距离看作其费用。这样就可以用Prim算法构造一棵最小生成树来解决问题。

graph

三、详细设计及运行结果

1.对图用邻接矩阵实现：以如下无向图为例 验证算法合理性，深度优先遍历：345127 广度优先遍历：345271

​ image-20240721122022588

image-20231228203321525

2.某公司拟建一个局域网，需要连接6栋楼（0，1，2，3，4，5），其地理分布如下图1所示，各边上的权值代表楼宇间距离。

image-20240721122131013

四、调试情况，设计技巧及体会

1.实验二关键算法：Prim构造最小生成树

①需要使用一个结构体数组，shortedge来存储各个顶点之间的最短路径，其中adjvex用于存储最短边所对应的的U中的点，lowcost是对应权值，也是当前最小的代价。②对shortedge数组写入初始信息，将起始点放入集合U中，即令shortedge[k].lowcost=0③对后续顶点处理，通过minimal函数找到最小路径所对应的顶点，输出最小路径信息，将该路径对应顶点放入集合U中，更新shortedge数组④关于minimal函数：只需要在当前数组中比较出lowcost最小的元素，返回它的下标loc即可 在vertex数组中找到该元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void MiniSpanTree_Prim(MGraph *G, VertexType start)
{
    int i, j, k;
    ShortEdge shortedge[VertexMax];
    // 处理初始点start
    k = LocateVex(G, start);
    for (i = 0; i < G->vexnum; i++)
    {
        shortedge[i].adjvex = start;
        shortedge[i].lowcost = G->AdjMatrix[k][i];
    }
    shortedge[k].lowcost = 0;
    // 2.处理后续结点
    for (i = 0; i < G->vexnum - 1; i++)
    {
        k = minimal(G, shortedge);                                                      // 找最短路径的顶点
        printf("%d->%d,%d\n", shortedge[k].adjvex, G->Vertex[k], shortedge[k].lowcost); // 输出找到的最短路径顶点及路径权值
        shortedge[k].lowcost = 0;                                                       // 将找到的最短路径顶点加入集合U中
        for (j = 0; j < G->vexnum; j++) // U中加入了新节点，可能出现新的最短路径，故更新short edge数组
        {
            if (G->AdjMatrix[k][j] < shortedge[j].lowcost)
            { // 有更短路径出现时，将其替换进short edge数组
                shortedge[j].lowcost = G->AdjMatrix[k][j];
                shortedge[j].adjvex = G->Vertex[k];
            }
        }
    }
}

2.关于一些输入scanf说明：

1
2
printf("请输入第%d条边信息及权值：", i + 1);
scanf(" %d,%d,%d", &v1, &v2, &w);
1
scanf(" %d", &start); // 有空格
1
2
3
4
5
printf("输入顶点元素（空格隔开）："); // 输入顶点元素
    for (i = 0; i < G->vexnum; i++)
    {
        scanf("%d", &G->Vertex[i]);
    }

五、源程序清单

1.在邻接表/邻接矩阵的基础上实现图的深度优先遍历和广度优先遍历操作，并输出遍历结果。

使用邻接矩阵存储图结构，并将邻接矩阵打印 算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
// 在邻接表/邻接矩阵的基础上实现图的深度优先遍历和广度优先遍历操作，并输出遍历结果。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define MaxVex 100    // 顶点数目最大值
typedef char VexType; // 顶点的数据类型
typedef int EdgeType; // 带权图中边上权值的数据类型

typedef struct
{
    VexType Vex[MaxVex];           // 顶点表
    EdgeType Edge[MaxVex][MaxVex]; // 邻接矩阵
    int vexnum, edgenum;           // 图的顶点数和边数
} MGraph;
/*----------创建无向图------------*/
void CreateGraph(MGraph *G)
{
    int i, j;
    int start, end; // 边的起点序号，终点序号
    int numV, numE;
    int w; // 边上的权值
    printf("请输入所创建无向图的顶点数和边数（用空格隔开）：");
    scanf("%d%d", &numV, &numE);
    G->vexnum = numV;
    G->edgenum = numE;

    printf("\n");
    // 图的初始化
    for (i = 0; i < G->vexnum; i++)
    {
        for (j = 0; j < G->vexnum; j++)
        {
            if (i == j)
            {
                G->Edge[i][j] = 0;
            }
            else
            {
                G->Edge[i][j] = 32767;
            }
        }
    }

    // 顶点信息存入顶点表
    for (i = 0; i < G->vexnum; i++)
    {
        printf("请输入第%d个顶点的信息：", i + 1);
        scanf("%d", &G->Vex[i]);
    }
    printf("\n");
    
    // 输入无向图边的信息
    for (i = 0; i < G->edgenum; i++)
    {
        printf("请输入边的顶点序号，终点序号，权值（用空格隔开）:");
        scanf("%d%d%d", &start, &end, &w);
        G->Edge[start - 1][end - 1] = w;
        G->Edge[end - 1][start - 1] = w; // 无向图的对称性
    }
}

/*--------打印出邻接矩阵-------------*/
void PrintMatrix(MGraph G)
{
    int i, j;
    printf("\n图的顶点为：");
    for (i = 0; i < G.vexnum; i++)
    {
        printf("%d ", G.Vex[i]);
    }
    printf("\n输出邻接矩阵：\n");
    printf("\t");
    for (i = 0; i < G.vexnum; i++)
    {
        printf("\t%8d", G.Vex[i]);
    }
    for (i = 0; i < G.vexnum; i++)
    {
        printf("\n\n%8d", G.Vex[i]);
        for (j = 0; j < G.vexnum; j++)
        {
            if (G.Edge[i][j] == 32767)
                printf("\t%9s", "∞");
            else
                printf("\t%8d", G.Edge[i][j]);
        }
        printf("\n");
    }
}

int main()
{
    MGraph G;
    CreateGraph(&G);
    PrintMatrix(G);
    system("pause");
    return 0;
}

深度优先遍历算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/****************深度优先遍历*******************/
int visitDFS[MaxVex];//在程序中先全局申明该数据，用于标记是否遍历过，初始时为0，遍历过将其标记为1.
void DFSTraverse(MGraph G)
{
    void DFS(MGraph G, int i);
    int i;
    printf("\n深度优先遍历序列为：");
    for (i = 0; i < G.vexnum; i++)
    {
        visitDFS[i] = 0;
    }
    for (i = 0; i < G.vexnum; i++)
    {
        if (!visitDFS[i])
        {
            DFS(G, i);
        }
    }
}
void DFS(MGraph G, int i)
{
    int j;
    visitDFS[i] = 1;
    printf("%d ", G.Vex[i]);
    for (j = 0; j < G.vexnum; j++)
    {
        if (G.Edge[i][j] != 32767 && !visitDFS[j])
            DFS(G, j);
    }
}

广度优先遍历算法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/****************广度优先遍历*******************/
// 队列
typedef struct
{
    int data[MaxVex];
    int front, rear;
} Queue;

// 初始化
void InitQueue(Queue *Q)
{
    Q->front = Q->rear;
}

// 判断队空
int IsEmpty(Queue *Q)
{
    if (Q->front == Q->rear)
        return 1;
    else
        return 0;
}

// 入队
void EnQueue(Queue *Q, int e)
{
    if ((Q->rear + 1) % MaxVex == Q->front)
        return;
    else
    {
        Q->data[Q->rear] = e;
        Q->rear = (Q->rear + 1) % MaxVex;
    }
}
// 出队
void DeQueue(Queue *Q, int *e)
{
    if (Q->rear == Q->front)
        return;
    else
    {
        *e = Q->data[Q->front];
        Q->front = (Q->front + 1) % MaxVex;
    }
}

// 广度优先遍历
int visitBFS[MaxVex];
void BFS(MGraph G)
{
    printf("\n广度优先遍历序列为：");
    int i, j;
    Queue Q;
    for (i = 0; i < G.vexnum; i++)
    {
        visitBFS[i] = 0;
    }
    InitQueue(&Q);
    for (i = 0; i < G.vexnum; i++)
    {
        if (!visitBFS[i])
        {
            visitBFS[i] = 1;
            printf("%d ", G.Vex[i]);
            EnQueue(&Q, i);

            while (!IsEmpty(&Q))
            {
                DeQueue(&Q, &i);
                for (j = 0; j < G.vexnum; j++)
                {
                    if (!visitBFS[j] && G.Edge[i][j] != 32767)
                    {
                        visitBFS[j] = 1;
                        printf("%d ", G.Vex[j]);
                        EnQueue(&Q, j);
                    }
                }
            }
        }
    }
    printf("\n");
}

主函数如下：

1
2
3
4
5
6
7
8
9
10
int main()
{
    MGraph G;
    CreateGraph(&G);
    PrintMatrix(G);
    DFSTraverse(G);
    BFS(G);
    system("pause");
    return 0;
}

2.某公司拟建一个局域网，需要连接6栋楼（0，1，2，3，4，5），其地理分布如下图1所示，各边上的权值代表楼宇间距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
// 某公司拟建一个局域网，需要连接6栋楼（0，1，2，3，4，5），其地理分布如下图1所示，各边上的权值代表楼宇间距离。
// 设计要求：根据下图中的楼宇分布，设计出布线造价最小的局域网络图，要求连接所有的顶点，并且总的布线费用最低。
// 实验提示：要想布线造价最小，可将图中各顶点间的距离看作其费用。这样就可以用Prim算法构造一棵最小生成树来解决问题。
// 顶点类型为整型
#include <stdio.h>
#include <stdlib.h>
#define VertexMax 20
#define MaxInt 32767

typedef int VertexType; // 每个顶点数据类型为整型

typedef struct
{ // 邻接矩阵结构体
    VertexType Vertex[VertexMax];
    int AdjMatrix[VertexMax][VertexMax]; // 邻接矩阵二维数组
    int vexnum, arcnum;
} MGraph;

typedef struct
{
    VertexType adjvex; // 候选最短边所依附的U中的点
    int lowcost;       // 候选最短边的权值
} ShortEdge;

int LocateVex(MGraph *G, VertexType v)
{ // 查找元素v在vertex[]中的下标，并返回下标
    int i;
    for (i = 0; i < G->vexnum; i++)
    {
        if (v == G->Vertex[i])
        {
            return i;
        }
    }
    printf("No such Vertex!\n");
    return -1;
}

void CreateUDN(MGraph *G)
{ // 构建无向网
    int i, j;
    printf("输入顶点个数和边数：\n"); //
    printf("顶点数 n=");
    scanf("%d", &G->vexnum);
    printf("边  数 n=");
    scanf("%d", &G->arcnum);
    printf("\n\n");

    printf("输入顶点元素（空格隔开）："); // 输入顶点元素
    for (i = 0; i < G->vexnum; i++)
    {
        scanf("%d", &G->Vertex[i]);
    }
    printf("\n");

    for (i = 0; i < G->vexnum; i++)
    { // 矩阵初始化
        for (j = 0; j < G->vexnum; j++)
        {
            G->AdjMatrix[i][j] = MaxInt;
        }
    }

    int n, m;
    VertexType v1, v2;
    int w;

    printf("请输入边的信息和权值(例如：1,2,15):\n");
    for (i = 0; i < G->arcnum; i++)
    {
        printf("请输入第%d条边信息及权值：", i + 1);
        scanf(" %d,%d,%d", &v1, &v2, &w);
        n = LocateVex(G, v1); // 获取v1所对应的在vertex数组中的下标
        m = LocateVex(G, v2); //
        if (n == -1 || m == -1)
        {
            printf("NO this vertex!\n");
            return;
        }
        G->AdjMatrix[n][m] = w;
        G->AdjMatrix[m][n] = w;
    }
}

void print(MGraph G)
{
    int i, j;
    printf("\n 邻接矩阵如下：\n");

    printf("\t ");
    for (i = 0; i < G.vexnum; i++)
    {
        printf("\t%d", G.Vertex[i]);
    }
    printf("\n\n");
    for (i = 0; i < G.vexnum; i++)
    {
        printf("\t%d", G.Vertex[i]);
        for (j = 0; j < G.vexnum; j++)
        {
            if (G.AdjMatrix[i][j] == MaxInt)
            {
                printf("\t∞");
            }
            else
                printf("\t%d", G.AdjMatrix[i][j]);
        }
        printf("\n");
    }
}

int minimal(MGraph *G, ShortEdge *shortedge)
{
    int i, j;
    int min, loc;

    min = MaxInt;
    for (i = 1; i < G->vexnum; i++)
    {
        if (min > shortedge[i].lowcost && shortedge[i].lowcost != 0)
        {
            min = shortedge[i].lowcost;
            loc = i;
        }
    }
    return loc;
}

void MiniSpanTree_Prim(MGraph *G, VertexType start)
{
    int i, j, k;
    ShortEdge shortedge[VertexMax];
    // 处理初始点start
    k = LocateVex(G, start);
    for (i = 0; i < G->vexnum; i++)
    {
        shortedge[i].adjvex = start;
        shortedge[i].lowcost = G->AdjMatrix[k][i];
    }
    shortedge[k].lowcost = 0;
    // 2.处理后续结点
    for (i = 0; i < G->vexnum - 1; i++)
    {
        k = minimal(G, shortedge);                                                      // 找最短路径的顶点
        printf("%d->%d,%d\n", shortedge[k].adjvex, G->Vertex[k], shortedge[k].lowcost); // 输出找到的最短路径顶点及路径权值
        shortedge[k].lowcost = 0;                                                       // 将找到的最短路径顶点加入集合U中

        for (j = 0; j < G->vexnum; j++) // U中加入了新节点，可能出现新的最短路径，故更新short edge数组
        {
            if (G->AdjMatrix[k][j] < shortedge[j].lowcost)
            { // 有更短路径出现时，将其替换进short edge数组
                shortedge[j].lowcost = G->AdjMatrix[k][j];
                shortedge[j].adjvex = G->Vertex[k];
            }
        }
    }
}

int main()
{
    VertexType start;
    MGraph G;
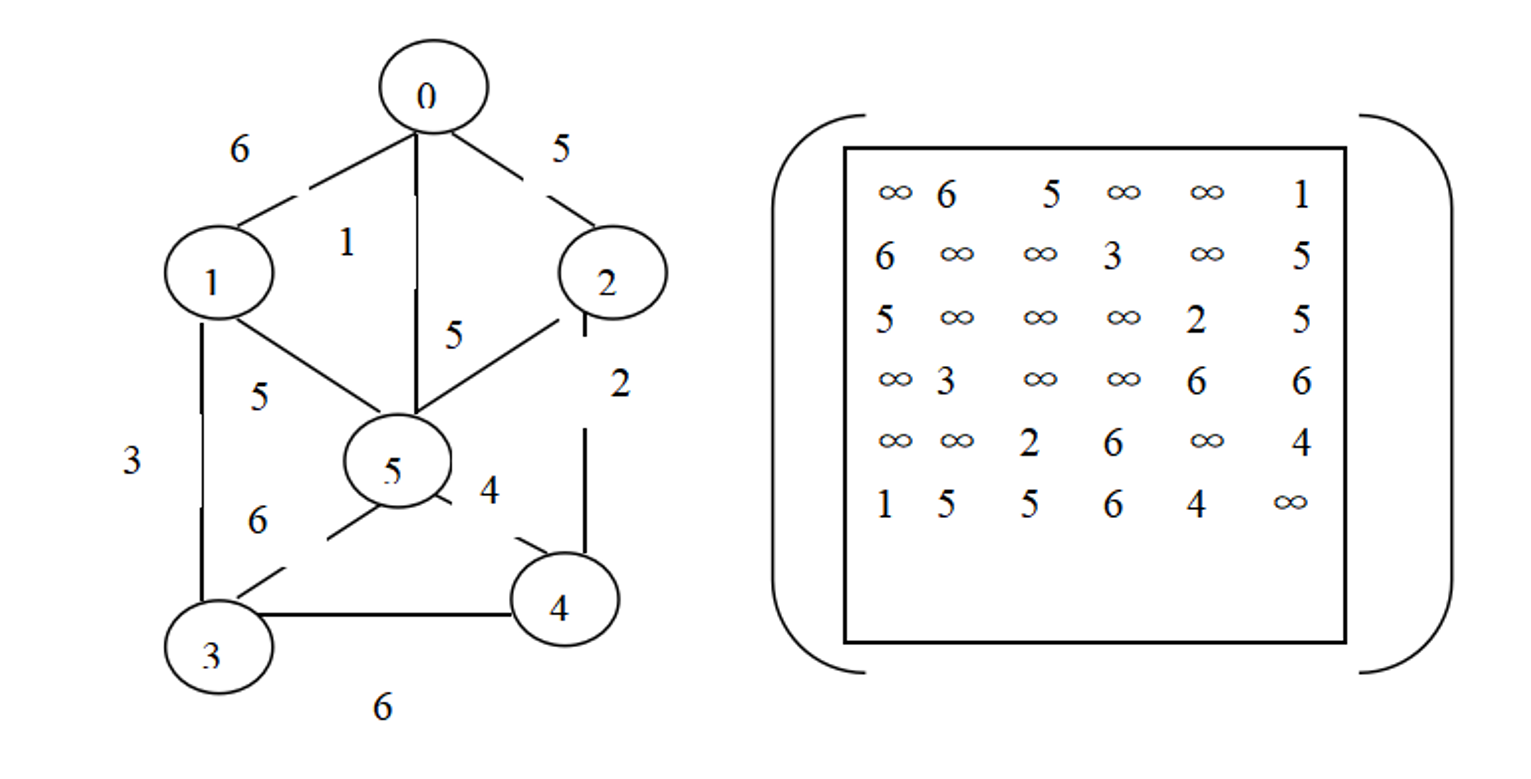
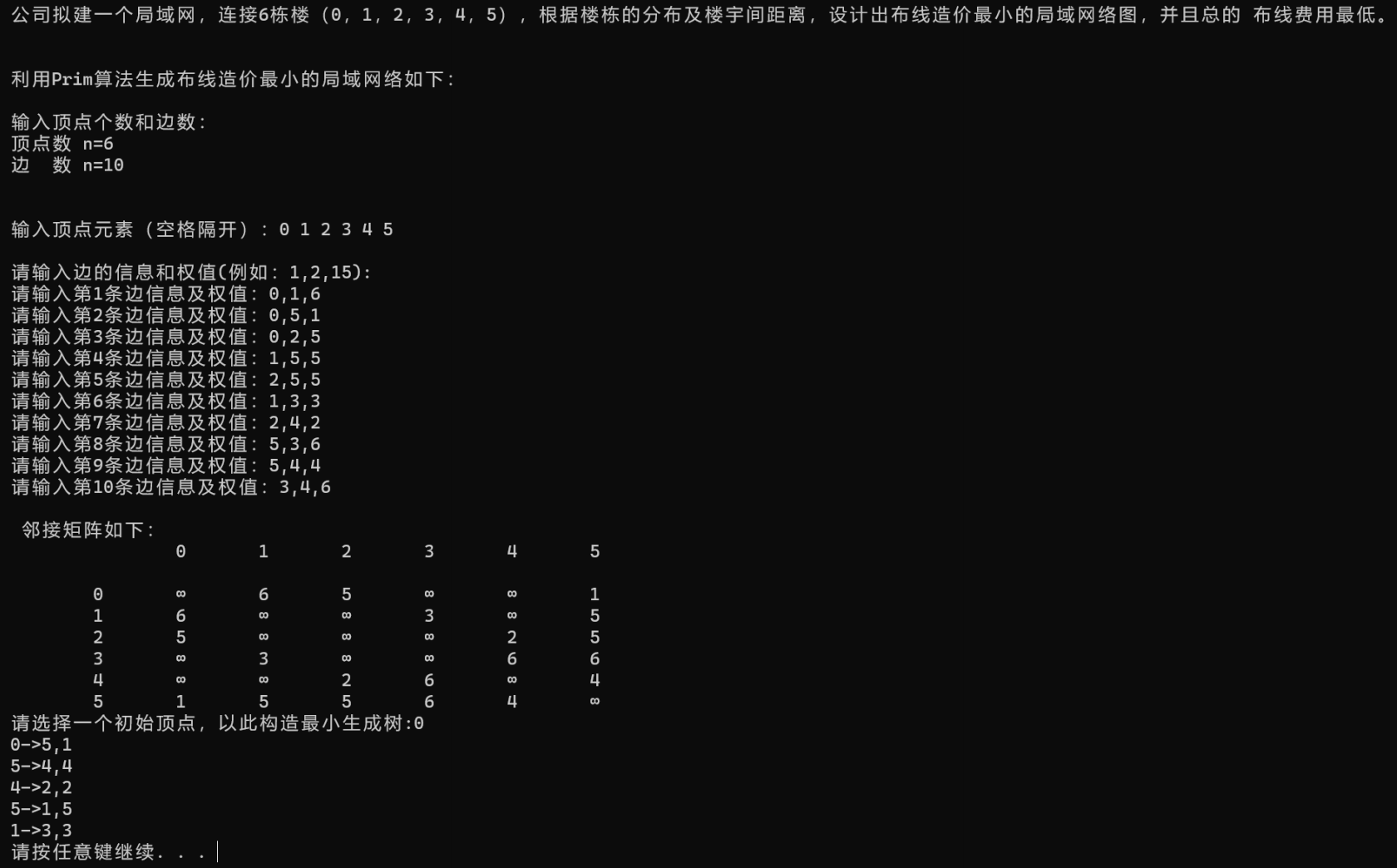
    printf("公司拟建一个局域网，连接6栋楼（0，1，2，3，4，5），根据楼栋的分布及楼宇间距离，设计出布线造价最小的局域网络图，并且总的布线费用最低。");
    printf("\n\n\n利用Prim算法生成布线造价最小的局域网络如下：\n\n");
    CreateUDN(&G);
    print(G);
    printf("请选择一个初始顶点，以此构造最小生成树:");
    scanf(" %d", &start); // 有空格
    MiniSpanTree_Prim(&G, start);
    system("pause");
    return 0;
}

上一篇：哈夫曼树 | Likt’s Blog (likt11.github.io)

下一篇： 数据结构期末复习 | Likt’s Blog (likt11.github.io)

-------------本文结束感谢您的阅读-------------