哈夫曼树及求Huffman编码

一、实验目的

掌握建立Huffman树及求Huffman编码的操作，加深对二叉树应用的理解。

二、实验内容

根据Huffman编码原理，编写一个在用户输入结点权重的基础上建立的Huffman编码程序。
程序设计思路：构造一棵Huffman树，由此得到的二进制前缀为Huffman编码
由于Huffman树没有度为1的结点，则一棵有n 个叶子结点的Huffman树共有2n-1个结点，设计一个结构数组，存储2n-1个结点的值，包括权重、双亲结点、左孩子和右孩子等。

三、详细设计及运行结果

四、调试情况，设计技巧及体会

该程序中，在构造哈夫曼树的函数中，使用p来对哈夫曼树每个结点进行操作，初始化时，需要HuffmanTree p = HT + 1;,因为HT对应于该结构的头结点，而本程序没有使用首个位置。

定义结构体如下：
// 对每一个结点，huffman树 该节点的结构定义
typedef struct
{
 int weight, parent, lchild, rchild;
} HfNode, *HuffmanTree;
typedef char **HuffmanCode; // 动态分配数组存储哈夫曼编码表。

select函数需要注意：获取最小两个权值的前提是，其parent为0,（作为条件）

五、源程序清单

// 根据Huffman编码原理，编写一个在用户输入结点权重的基础上建立的Huffman编码程序。
#include <stdlib.h>
#include <string.h>
#include <stdio.h>

// 对每一个结点，huffman树 该节点的结构定义
typedef struct
{
    int weight, parent, lchild, rchild;
} HfNode, *HuffmanTree;
typedef char **HuffmanCode; // 动态分配数组存储哈夫曼编码表。

// 构造哈夫曼树
// HT为一棵哈夫曼树，HC用来存储n个字符的哈夫曼编码，w设为一个数组，存储这n个结点的权值，n个字符
void CreatHfTree(HuffmanTree &HT, HuffmanCode &HC, int *w, int n)
{
    void Select(HuffmanTree & HT, int s, int &s1, int &s2);
    int m = 2 * n - 1;
    HT = (HuffmanTree)malloc((m + 1) * sizeof(HfNode));
    HuffmanTree p = HT + 1;
    for (int i = 1; i <= n; ++i, ++p)
    {
        *p = {w[i - 1], 0, 0, 0};
    } // 初始化了n个结点
    for (int i = n + 1; i <= m; ++i, ++p)
    {
        *p = {0, 0, 0, 0};
    } // 初始化了合并后生成的n-1个结点
    for (int i = n + 1; i <= m; ++i)
    {
        int s1, s2;
        Select(HT, i - 1, s1, s2);
        HT[i].weight = HT[s1].weight + HT[s2].weight;
        HT[s1].parent = i;
        HT[s2].parent = i;
        HT[i].lchild = s1;
        HT[i].rchild = s2;
    } // 创建哈夫曼树
    //-------从叶子到根逆向求每个字符的哈夫曼编码-------
    HC = (HuffmanCode)malloc((n + 1) * sizeof(HuffmanCode));
    char *cd = (char *)malloc(n * sizeof(char));
    cd[n - 1] = '\0';
    for (int t = 1; t <= n; ++t)
    {
        int start = n - 1;
        for (int c = t, f = HT[c].parent; f != 0; c = f, f = HT[f].parent)
        {
            if (c == HT[f].lchild)
            {
                cd[--start] = '0';
            }
            else
            {
                cd[--start] = '1';
            }
        }
        HC[t] = (char *)malloc((n - start) * sizeof(char));
        strcpy(HC[t], &cd[start]);
    }
    free(cd);
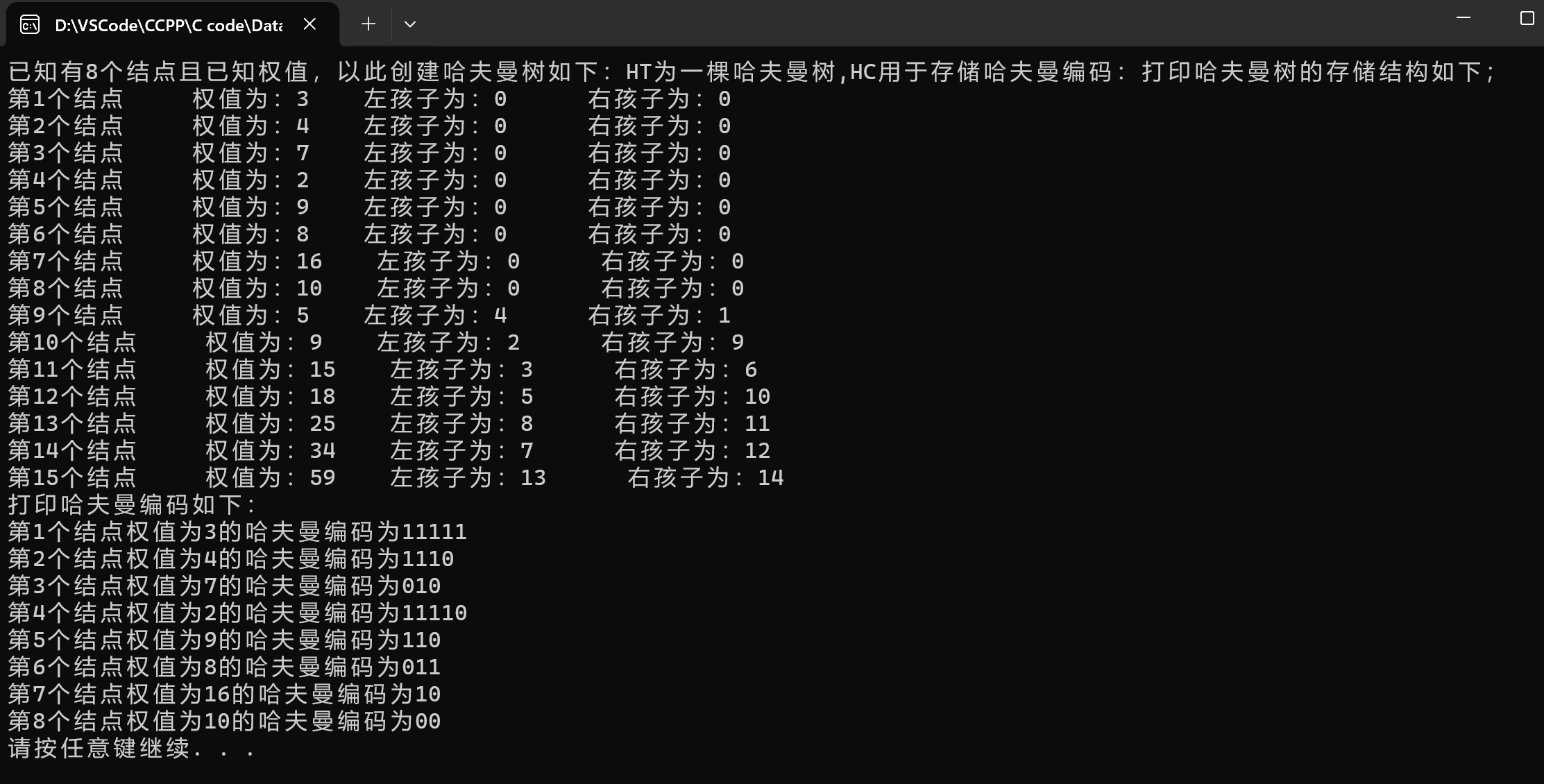
    printf("打印哈夫曼树的存储结构如下；\n");
    for (int x = 1; x <= m; ++x)
    {
        printf("第%d个结点     权值为：%d    左孩子为：%d      右孩子为：%d     \n", x, HT[x].weight, HT[x].lchild, HT[x].rchild);
    }
    printf("打印哈夫曼编码如下：\n");
    for (int j = 1; j <= n; ++j)
    {
        printf("第%d个结点权值为%d的哈夫曼编码为%s\n", j, HT[j].weight, HC[j]);
    }
}

// 求一棵哈夫曼树结点下标小于s的最小的两个结点，用s1,s2返回他们的下标

void Select(HuffmanTree &HT, int s, int &s1, int &s2)
{
    s1 = 0;
    s2 = 0;
    for (int i = 1; i <= s; ++i)
    {
        if (HT[i].parent == 0)
        {
            if (s1 == 0 || HT[i].weight < HT[s1].weight)
            {
                s2 = s1;
                s1 = i;
            }
            else if (s2 == 0 || HT[i].weight < HT[s2].weight)
            {
                s2 = i;
            }
        }
    }
}
int main()
{
    int n = 8;
    int w[8] = {3, 4, 7, 2, 9, 8, 16, 10};
    HuffmanTree HT;
    HuffmanCode HC;
    printf("已知有%d个结点且已知权值，以此创建哈夫曼树如下：", n);
    printf("HT为一棵哈夫曼树,HC用于存储哈夫曼编码：");
    CreatHfTree(HT, HC, &w[0], n);
    system("pause");
    return 0;
}

上一篇：二叉树 | Likt’s Blog (likt11.github.io)

下一篇：图及其应用 | Likt’s Blog (likt11.github.io)