构造二叉链表树实验报告

一、实验目的

熟练掌握树的基本概念、定义和性质。
熟练掌握二叉树的二叉链表存储结构，以及二叉树的各种基本操作。
掌握构造二叉链表树的不同算法，能够从输入数据构造二叉树。
掌握遍历二叉树的三种递归算法。
学习利用栈/队列实现二叉树的非递归遍历操作。
能够对二叉树遍历操作加以灵活应用，实现计算二叉树的结点、计算二叉树的深度和计算二叉树叶子结点的算法。
进一步加深对二叉树结构和性质的理解，逐步培养解决实际问题的编程能力。

二、实验内容

从输入数据的基础上建立二叉链表树，并实现二叉树抽象类型定义中的基本操作。
分别调用先序、中序和后序遍历递归算法对二叉链表树进行遍历，对比各种不同遍历算法的结果。
尝试使用不同的存储结构存储二叉树，例如顺序存储，并能够实现两种存储结构之间的转换。
用非递归方法实现二叉树的遍历操作。
实现计算二叉树的深度的算法。
实现计算二叉树的叶子结点数的算法。

三、详细设计及运行结果

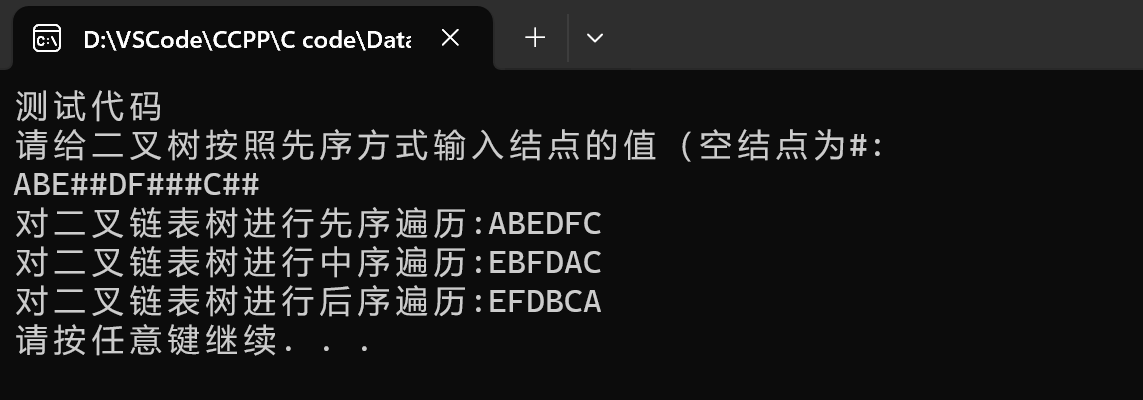
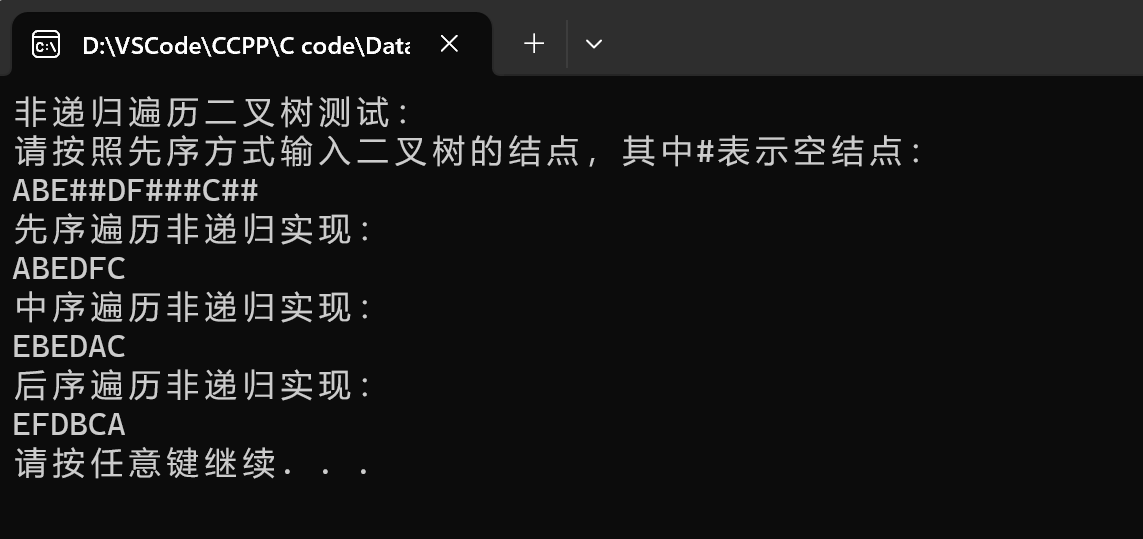
依据以下二叉树进行测试实验，首先按照先序序列ABE##DF###C##对该二叉链表树进行输入。对其进行先序遍历：ABEDFC，中序遍历： EBFDAC，后序遍历：EFDBCA

graph TD
A-->B;
A-->C;
B-->D;
B-->E;
E-->3#;
E-->4#;
D-->F;
D-->#;
C-->1#;
C-->2#;
F-->7#;
F-->8#;

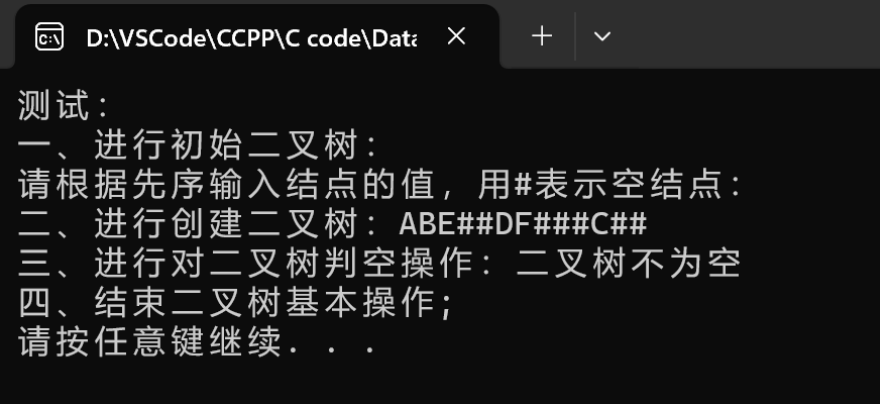
建立二叉链表树，并进行二叉树的基本操作。
分别调用先序、中序和后序遍历递归算法对二叉链表树进行遍历，对比各种不同遍历算法的结果。
非递归遍历二叉树算法：
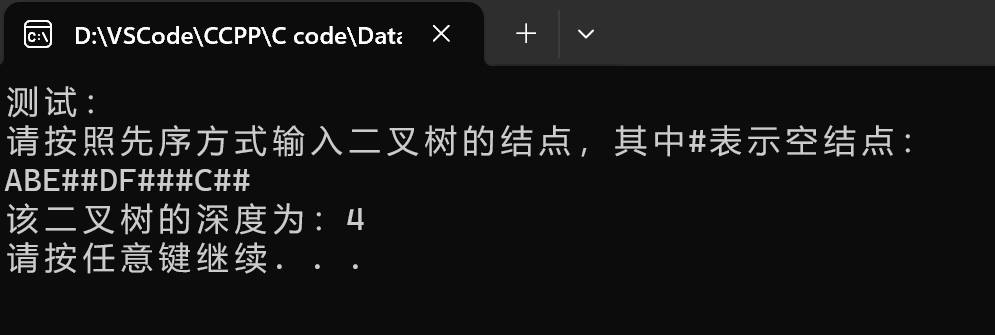
二叉树深度的算法：
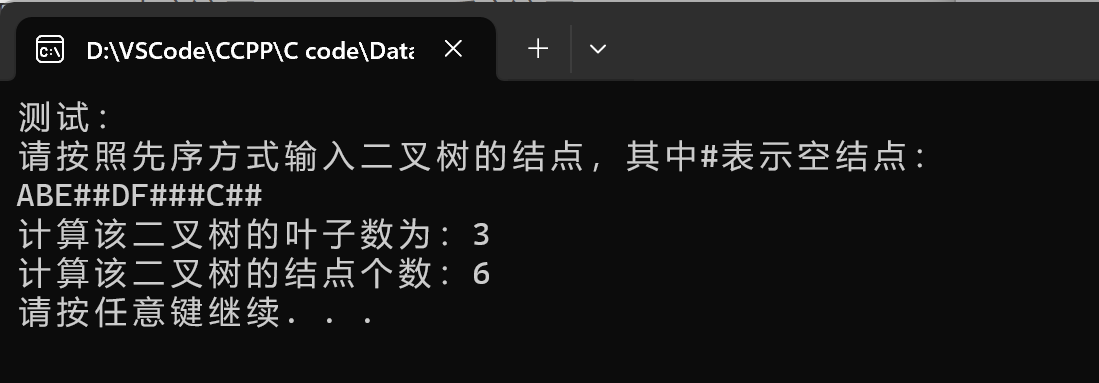
计算二叉树叶子结点的个数算法：

四、调试情况，设计技巧及体会

对于指针的使用&和*区别
二叉树的非递归遍历：
- 前序遍历：①首先建立一个二维指针，用来存储每个结点的地址，定义栈顶指针top，初始值为-1，并将根结点存入栈中，top++。②进入while循环，栈顶指针不为-1，则进入while循环，输出当前栈顶元素p的数据域，代表前序遍历的第一个节点为根结点。③如果当前的p结点拥有右子树，将这个右子树存入栈中，没有则不存；因为栈的特点是先进后出，所以先存右子树，再存左子树。④如果当前P结点拥有左子树，将这个左子树结点存入栈中，没有则不存。⑤如果这个结点为叶子结点，要么直接将这个结点输出，不需要存结点。⑥再判断top是否为-1，之后再重复执行2,3,4步骤。
- 中序遍历：①与非递归前序遍历相同，同样需要一个二维指针的栈，栈顶元素初始化为-1。② 首先判断if的判断条件，这个二叉树不为空；③在进入if条件语句中的while循环，这个循环是将与根结点相连的所有左子树全部存入栈中；
  ④退出循环后，在判断第二个while循环的条件，栈不为空，则进入while循环；⑤首先输出距离与根结点相连最远的左子树；⑥如果这个结点拥有右子树，先将这个右子树结点存入栈中；⑦点是否拥有左子树，有的话，将与这个结点相连的所有左子树存入栈中，没有就不执行while循环，并且结束判断结点是否拥有右子树的循环；⑧在判断top是否为-1，成立进入循环，重复上述步骤即可； 存储总结：就是一直将与根结点的所有左子树存入栈中，判断左后一个结点是否拥有右子树，有的话就把与这个结点相连的所有左子树存入栈中；
- 后序遍历：① 同样建立一个二维指针的栈，用来存储每个结点的地址； ② 进入do-while循环，首先，将与根结点相连的所有左子树都存入栈中；③将BitTree类型的指针p赋空，判断while循环是否成立； ④如果这个最后一个结点的右子树==p，则输出当前结点的数据域，栈顶指针—；⑤并将这个结点赋给指针p表示这个结点已经访问过，并且已经输出；⑥如果当前结点的右子树!=p，则接着访问这个结点的右子树，并且结束while循环，判断do-while循环的判断条件；⑦重复上述过程，知道不满足do-while循环的判断条件；存储总结：先将与根结点相连的所有左子树全部存入栈中，在判断左后一个结点是否有右子树，如果有则访问这个结点，没有的话就输出当前结点。（当do-while循环中的两个while循环完成后，在判断do-while循环的条件，之后重复上述过程，直到不满足do-while循环条件；）

五、源程序清单

在输入数据的基础上建立二叉链表树，并实现二叉树抽象类型定义中的基本操作。

// 从输入数据的基础上建立二叉链表树，并实现二叉树抽象类型定义中的基本操作。
#include <string.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct BiTNode
{
    char data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

void InitBiTree(BiTree *T) // 初始化二叉树
{
    printf("一、进行初始二叉树：");
    (*T)->data = NULL;
    (*T)->lchild = NULL;
    (*T)->rchild = NULL;
}
void CreatBiTree(BiTree *T) // 二级指针写法创建二叉树的结点
{
    char ch;
    scanf("%c", &ch);
    if (ch == '#')
    {
        *T = NULL;
    }
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = ch;
        CreatBiTree(&(*T)->lchild);
        CreatBiTree(&(*T)->rchild);
    }
}
void IsTempty(BiTree T) // 判断二叉树是否为空
{
    printf("三、进行对二叉树判空操作：");
    if (T->data == NULL)
    {
        printf("二叉树为空\n");
    }
    else
    {
        printf("二叉树不为空\n");
    }
}

int main()
{
    printf("测试：\n");
    BiTree T;
    T = (BiTree)malloc(sizeof(BiTNode));
    InitBiTree(&T); // 初始化二叉树
    printf("\n请根据先序输入结点的值，用#表示空结点：\n");
    printf("二、进行创建二叉树：");
    CreatBiTree(&T); // 创建二叉树
    IsTempty(T);     // 判断二叉树是否为空
    printf("四、结束二叉树基本操作;\n");
    system("pause");
    return 0;
}

分别调用先序、中序和后序遍历递归算法对二叉链表树进行遍历，对比各种不同遍历算法的结果。

// 分别调用先序、中序和后序遍历递归算法对二叉链表树进行遍历，对比各种不同遍历算法的结果。

#include <string.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct BiTNode
{
    char data;
    struct BiTNode *lchild;
    struct BiTNode *rchild; // 左右孩子指针。
} BiTNode, *BiTree;

void CreatBiTree(BiTree *T) // 创建二叉链表树
{
    char ch;
    scanf("%c", &ch);
    if (ch == '#')
    {
        *T = NULL; // null表示为空枝
    }
    else
    {
        *T = (BiTNode *)malloc(sizeof(BiTNode));
        (*T)->data = ch;            // 根结点    T是指向bitree的一个指针，*T即为指向的那个Bitree变量，其中Bitree又是指向btinode的指针，对该指针取值&即为
        CreatBiTree(&(*T)->lchild); // 构造左子树
        CreatBiTree(&(*T)->rchild); // 构造右子树
    }
}

void PrintElement(char e) // visit()函数
{
    printf("%c", e);
}

void PreOrderTraverse(BiTree T) // 先序遍历
{
    if (T)
    {
        PrintElement(T->data);
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}
void InOrderTraverse(BiTree T) // 中序遍历
{
    if (T)
    {
        InOrderTraverse(T->lchild);
        PrintElement(T->data);
        InOrderTraverse(T->rchild);
    }
}
void PostOrderTraverse(BiTree T) // 后序遍历
{
    if (T)
    {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        PrintElement(T->data);
    }
}

int main()
{
    printf("测试代码\n");
    BiTree T;//T为BiTree类型的变量，即为指向BiTNode类型的指针，
    T = (BiTree)malloc(sizeof(BiTNode));//为T开辟一个空间
    printf("请给二叉树按照先序方式输入结点的值（空结点为#:\n");
    CreatBiTree(&T);//将T的地址作为实参传入CreatBiTree函数，
    printf("对二叉链表树进行先序遍历:");
    PreOrderTraverse(T);
    printf("\n对二叉链表树进行中序遍历:");
    InOrderTraverse(T);
    printf("\n对二叉链表树进行后序遍历:");
    PostOrderTraverse(T);
    printf("\n");
    system("pause");
    return 0;
}

用非递归方法实现二叉树的遍历操作。

//用非递归方法实现二叉树的遍历操作。
#include <stdio.h>
#include <stdlib.h>
#define N 20

typedef struct tree
{
    char ch;
    struct tree *lchild;
    struct tree *rchild;
} BitTree;

BitTree *CreateTree() // 创建二叉树，利用递归的方法
{
    BitTree *bt;
    char str;
    scanf("%c", &str);
    if (str == '#')
    {
        return NULL;
    }
    else
    {
        bt = (BitTree *)malloc(sizeof(BitTree));
        bt->ch = str;
        bt->lchild = CreateTree();
        bt->rchild = CreateTree();
        return bt;
    }
}

// 前序遍历的非递归实现
// 利用栈来实现，根结点进栈，之后栈非空，弹出，接着根结点的右节点进栈，之后，左节点进栈，接着弹出栈顶元素。
// 此结点的右节点进栈，之后左节点进栈，弹出栈顶元素（输出）……一直这样下去。直到栈为空。
void PreOrder(BitTree *bt)
{
    BitTree **s;
    BitTree *p;
    int top = -1;
    // 创建栈
    s = (BitTree **)malloc((N + 1) * sizeof(BitTree *));
    // 初始化栈
    s[++top] = bt;
    // 非递归前序遍历
    while (top != -1)
    {
        p = s[top--];
        printf("%c", p->ch); // 栈的特点，先进后出。
        if (p->rchild)
            s[++top] = p->rchild;
        if (p->lchild)
            s[++top] = p->lchild;
    }
    free(s);
}
// 中序遍历，非递归实现
// 思想：利用栈，从根结点开始循环，只要有左节点就进栈，直到左子节点为空，接着弹出栈顶输出，判断该节点是否有右子节点。若有则进栈，若没有继续弹栈。
void InOrder(BitTree *bt)
{
    BitTree **s;
    BitTree *p, *q;
    int top = -1;
    s = (BitTree **)malloc((N + 1) * sizeof(BitTree *));
    if (bt)
    {
        while (bt)
        {
            s[++top] = bt;
            bt = bt->lchild;
        }
        while (top != -1)
        {
            p = s[top--];
            printf("%c", p->ch);
            while (p->rchild)
            {
                s[++top] = p->rchild;
                q = p->rchild;
                while (q->lchild)
                {
                    s[++top] == q->lchild;
                    q = q->lchild;
                }
                break;
            }
        }
    }
}

void PostOrder(BitTree *bt) // 后序遍历，非递归实现
{
    BitTree **s;
    BitTree *p;
    int top = -1;
    s = (BitTree **)malloc((N + 1) * sizeof(BitTree *));
    do
    {
        while (bt) // 一直遍历左子树直到该左子树的左孩子空为止
        {
            s[++top] = bt;   // 将所有左孩子存入栈中
            bt = bt->lchild; // 指向下一个左子树。
        }
        p = NULL;
        while (top != -1)
        {
            bt = s[top];
            if (bt->rchild == p) // p:表示为null，或者右子节点被访问过来。
            {
                printf("%c", bt->ch); // 输出节点数据域
                top--;                //
                p = bt;               // p记录下刚刚访问过的节点
            }
            else
            {
                bt = bt->rchild; // 访问右子树结点
                break;
            }
        }

    } while (top != -1);
}

int main()
{
    printf("非递归遍历二叉树测试：\n");
    printf("请按照先序方式输入二叉树的结点，其中#表示空结点：\n");
    BitTree *btr = CreateTree();
    printf("先序遍历非递归实现：\n");
    PreOrder(btr);
    printf("\n中序遍历非递归实现：\n");
    InOrder(btr);
    printf("\n后序遍历非递归实现：\n");
    PostOrder(btr);
    printf("\n");
    system("pause");
    return 0;
}

实现计算二叉树的深度的算法。

#include <stdlib.h>
#include <stdio.h>
#include <string.h>

typedef struct BiTNode
{
    char data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

void CreatBiTree(BiTree *T) // 创建二叉链表树
{
    char ch;
    scanf("%c", &ch);
    if (ch == '#')
    {
        *T = NULL; // null表示为空枝
    }
    else
    {
        *T = (BiTNode *)malloc(sizeof(BiTNode));
        (*T)->data = ch;            // 根结点      T是指向bitree的一个指针，*T即为指向的那个Btree变量，其中Bitree又是执行binode的指针，对该指针取值&即为
        CreatBiTree(&(*T)->lchild); // 构造左子树
        CreatBiTree(&(*T)->rchild); // 构造右子树
    }
}

int DeepBiTree(BiTree T) // 求二叉树的深度
{
    int lnum, rnum;
    if (T == NULL)
    {
        return 0;
    }
    else
    {
        lnum = DeepBiTree(T->lchild);
        rnum = DeepBiTree(T->rchild);
        return (lnum > rnum ? lnum : rnum) + 1;
    }
}
int main()
{
    printf("测试：\n");
    BiTree T;
    T = (BiTree)malloc(sizeof(BiTNode));
    printf("请按照先序方式输入二叉树的结点，其中#表示空结点：\n");
    CreatBiTree(&T);
    printf("该二叉树的深度为：%d\n", DeepBiTree(T));
    system("pause");
    return 0;
}

实现计算二叉树的叶子结点数的算法。

#include <stdlib.h>
#include <stdio.h>
#include <string.h>

typedef struct BiTNode
{
    char data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

void CreatBiTree(BiTree *T)
{
    char ch;
    scanf("%c", &ch);
    if (ch == '#')
    {
        *T = NULL;
    }
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        (*T)->data = ch;
        CreatBiTree(&(*T)->lchild);
        CreatBiTree(&(*T)->rchild);
    }
}
int LeafBiTree(BiTree T) // 二叉树求叶子数
{
    if (T == NULL)
    {
        return 0;
    }
    else if (T->lchild == NULL && T->rchild == NULL)
    {
        return 1;
    }
    else
    {
        return LeafBiTree(T->lchild) + LeafBiTree(T->rchild);
    }
}

int NodeBiTree(BiTree T) // 统计二叉树的结点个数
{
    if (T == NULL)
    {
        return 0;
    }
    else
    {
        return (NodeBiTree(T->lchild) + NodeBiTree(T->rchild)) + 1;
    }
}
int main()
{
    printf("测试：\n");
    BiTree T;
    T = (BiTree)malloc(sizeof(BiTNode));
    printf("请按照先序方式输入二叉树的结点，其中#表示空结点：\n");
    CreatBiTree(&T);
    printf("计算该二叉树的叶子数为：%d\n", LeafBiTree(T));
    printf("计算该二叉树的结点个数：%d\n", NodeBiTree(T));
    system("pause");
    return 0;
}

下一篇：哈夫曼树 | Likt’s Blog (likt11.github.io)